iSoSuG - intelligentes Sondesuchoskop
| iSoSuG | |
|---|---|
| Ein intelligentes Sondesuchoskop, was es erlaubt, mit mehreren Leuten fuchsjagdähnliche Aufgaben zu erledigen | |
| Mitarbeiter | Stefan, DK3SB Sebastian, DL3YC Severin, DK1SEV |
| Status | auf Eis bis weitere Erkenntnisse vorliegen |
Suchoskop (nur Feldstärkeindikator) ist am Boom der Antenne befestigt. Zusätzlich gibt es eine kleine Einheit aus folgenden Bestandteilen:
- Kompass ST LIS3MDL
- GPS uBlox MAX-M8Q
- Sender/Empfänger und Prozessor (CC430F5133?)
- UI (Text-Display, Taster)
- HD44780
Das Display sollte möglichst wenig breit sein, um die Unit Antennenboomtauglich zu gestalten. LCD 2×8 bietet sich an, z.B. das hier. Ein Plastikgehäuse ist wichtig, damit der Kompass nicht gestört wird.
Man kann mit beliebig vielen Leuten suchen. Man peilt immer die größte Feldstärke und drückt auf den Knopf, um einen Messwert (Position, Peilrichtung) abzuspeichern und zu übertragen. Durch Kreuzpeilung mit mehreren Leuten wird die wahrscheinlichste Position ausgerechnet aus allen Punkten und auf dem Display aktuelle Richtung, Sollrichtung und Entfernung dorthin angezeigt. Der Witz ist, dass bei allen Leuten alle Position empfangen werden und so alle auf den gleichen Punkt zulaufen können, und sich (im Bestfall) alle bei der Sonde treffen. Vielleicht kann man so die erfahrenen Sucher ausstechen. (Was zu beweisen wäre)
BOM
| Teil | Quelle | Preis |
|---|---|---|
| CC430 | Sample | 7€ |
| LCD 8×2 | ebay | 7€ |
| LIS3MDL | Sample | 2€ |
| GEH KS 35 | Reichelt | 1,50 |
| Filter,Balun | Mouser | 3€? |
| Akku | Pollin | 3€ |
| Gesamt | 25€ |
Power Budget
| Komponente | Stromaufnahme [mA] | Leistungsaufnahme [mW] |
|---|---|---|
| LCD | 20 @ 5V | 100 |
| CPU + RF | 20(30) @ 3.3V | 66 (99) |
| Kompass | 1 @ 3.3V | 4 |
| GPS | 25 @ 3.3V | 83 |
| Summe | - | 255 (290) |
Der 3V-Regler muss mindestens 60 mA liefern können, der 5V-Regler mindestens 30 mA. Werden für die beiden Regler Effizienzen von 75% angesetzt, ergibt sich die Gesamtleistungsaufnahme zu 340mW im Empfangs- und 390mW im Sendefall. Ein Teebeutel (7,2V, 820mAh, 5,9Wh) hält damit dann etwa 17 Stunden durch.
Notwendige Berechnungen mit Koordinaten
Es ist notwendig, diverse Berechnungen durchzuführen, um den wahrscheinlichsten Sondenpunkt zu erhalten und eine Navigation auf dem kürzesten Weg dahin durchzuführen. Wichtig bei den Formeln von Williams: WEST und NORD haben positive Vorzeichen, OST und SÜD negative! Alle Winkel sind im Bogenmaß einzusetzen.
Grundlage sind eine Menge von Punkten und dazugehörigen Peilrichtungen, sowie die eigene (aktuelle) GPS-Position. Der Algorithmus berechnet beim Hinzufügen eines neuen Peilvektors die wahrscheinlichste Sondenposition:
Berechnung des wahrscheinlichsten Sondenpunktes aus N Koordinaten und N Richtungen Algorithmus: zuerst die Schnittpunkte aller Vektoren berechnen, siehe http://williams.best.vwh.net/avform.htm#Intersection. Diese Schnittpunkte können danach (ohne großartige weitere Ungenauigkeiten) einfach Arithmetisch gemittelt werden, um auf das „Center of Gravity“ zu kommen. Der gemachte Fehler dabei ist sehr klein, siehe http://www.geomidpoint.com/calculation.html.
Berechnung Entfernung/Peilrichtung zwischen zwei Punkten Grundlage: Haversine Formula - Es wird aus dem wahrscheinlichsten Sondenpunkt und der aktuellen GPS-Position damit die Richtung und Entfernung ausgerechnet. Siehe http://williams.best.vwh.net/avform.htm#Dist und http://williams.best.vwh.net/avform.htm#Crs.
Evaluierung des Algorithmus
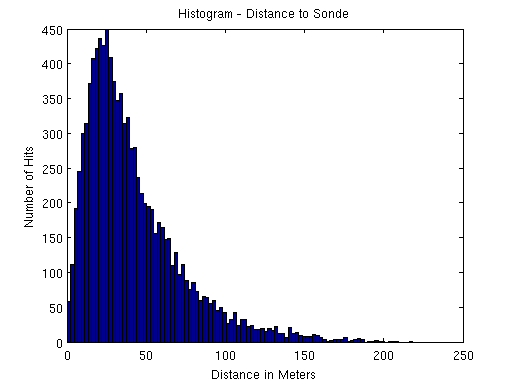
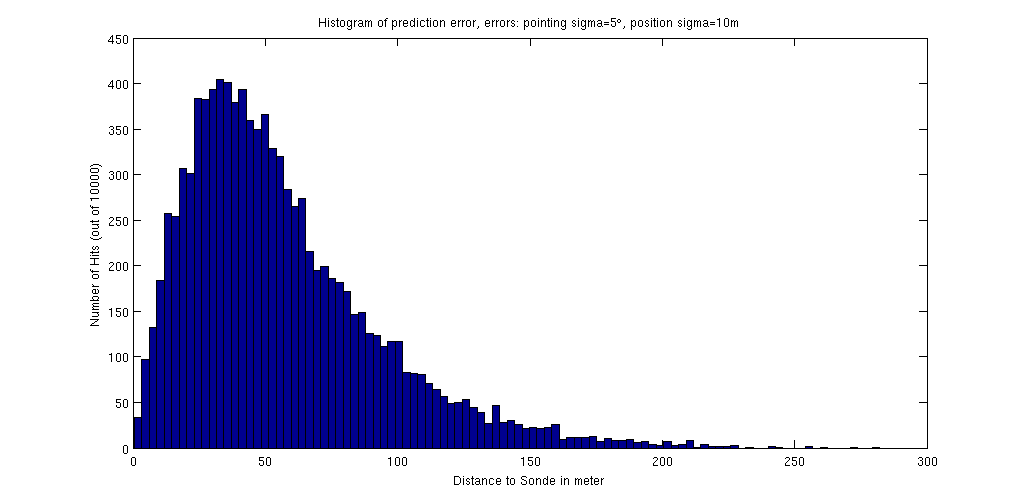
Es wurde eine Sondensuche simuliert - d.h. ein Sondenpunkt festgelegt, sowie sechs Peilpositionen. Eine MATLAB-Simulation (algorithm.m) berechnet den wahren Kurs (distbear.m) von jedem Punkt zur Sonde und versieht ihn mit einer normalverteilten „Fehlpeilung“ (mit Standardabweichung von 5°). 68% der gemessenen Winkel liegen damit im Bereich +-5° zur realen Richtung. Die Position wird vorher mit einem normalverteilten Fehler (GPS) von sigma=10m beaufschlagt.
Es wird nun für jede Punkt-Richtungs-Kombination der Schnittpunkt berechnet (intersection.m). Sollte dies für einen Punkt nicht erfolgreich sein (parallele Strecken, kein Schnittpunkt, unendlich Schnittpunkte) oder der Abstand zum Sollwert (später: zur eigenen Position) viel zu groß sein („fast parallele Strecken“) wird er ignoriert. Mit 6 Peilpunkten ergeben sich maximal 15 Punkte, die in die Rechnung einfließen können.
Danach wird Länge und Breite aller Schnittpunkte arithmetisch gemittelt und es ergibt sich der wahrscheinliche Sondenpunkt. Die Distanz zum realen Punkt in Metern wird berechnet und ausgegeben.
Eine einfache Schleife lässt diesen Algorithmus zehntausend mal laufen, um statistisch aussagekräftige Werte zu erhalten (statistics.m). Mit hist() kann hinterher die Entfernungsverteilung erzeugt werden.
Es zeigen sich gutartige Ergebnisse, mit einer durchschnittlichen Entfernung von etwa 50m um den Zielpunkt. Es zeigt sich keine Normalverteilung um den korrekten Zielpunkt (wie man vielleicht erwarten könnte), sondern eine Chi-Verteilung (Wurzel der Quadrate der normalverteilten Zufallsvariablen X und Y).